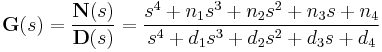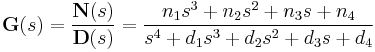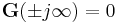Strictly proper

In control theory, a strictly proper transfer function is a transfer function where the degree of the numerator is less than the degree of the denominator.

Example

The following transfer function is not strictly proper

\textbf{G}(s) = \frac{\textbf{N}(s)}{\textbf{D}(s)} = \frac{s^{4} %2B n_{1}s^{3} %2B n_{2}s^{2} %2B n_{3}s %2B n_{4}}{s^{4} %2B d_{1}s^{3} %2B d_{2}s^{2} %2B d_{3}s %2B d_{4}}

because

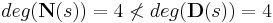deg(\textbf{N}(s)) = 4 \nless deg(\textbf{D}(s)) = 4 .

The following transfer function however, is strictly proper

\textbf{G}(s) = \frac{\textbf{N}(s)}{\textbf{D}(s)} = \frac{n_{1}s^{3} %2B n_{2}s^{2} %2B n_{3}s %2B n_{4}}{s^{4} %2B d_{1}s^{3} %2B d_{2}s^{2} %2B d_{3}s %2B d_{4}}

because

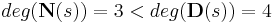deg(\textbf{N}(s)) = 3 < deg(\textbf{D}(s)) = 4 .

Implications

A strictly proper transfer function will approach zero as the frequency approaches infinity.

\textbf{G}(\pm j\infty) = 0

which is true for all physical processes.

See also